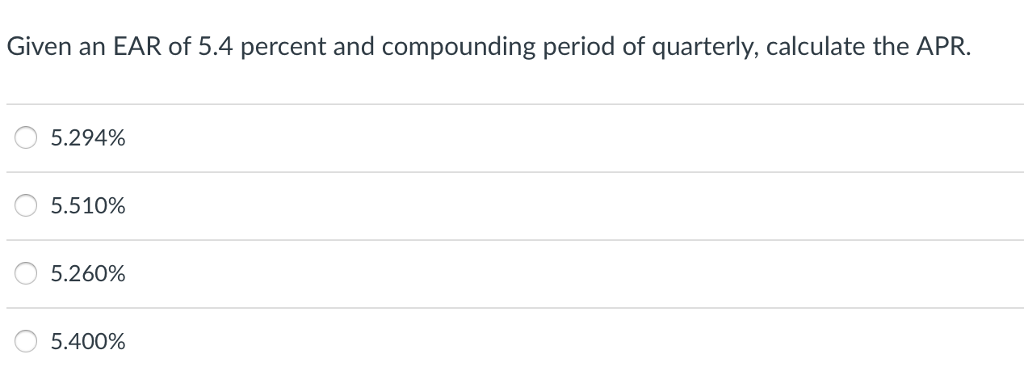
So we started off that topic by introducing the concept with some intuition.
But before doing so, I want to briefly review our first topic, Time Value of Money. Today, we're going to be turning to a new topic, interest rates.
Apr and ear practice problems how to#
In this topic, interest rates, I want to start off by talking about interest rate quoting conventions and I want to talk about how to compute the present value and future value of string of cash flow when they arrived at irregular time, non-annual and when the compounding is not annual as well. We discussed some useful shortcuts to compute the present value and the future value of cash flow streams that we commonly come across in practice, streams like an annuity and a perpetuity and then we close out the topic by talking about taxes and inflation and their impact on our dollar returns and our ability to consume goods and services. Namely, the discount factor and the timeline, then we applied those tools to move money back in time via discounting and forward in time via compounding. As you'll recall, we started off with some intuition, then we introduced the tools associated with the time value of money. But before doing so, I want to briefly review our last topic, the time value of money. Today, we're going to turn to a new topic, interest rates.
when i = APR N = total compounding periods - then multiply by m (periods/year) to get an annualized number.Welcome back to Corporate Finance. Depending on which i you want your calculator to give you, you'll need to use the corresponding N. There is actually one more step you would need to put into your calculator which would be to make that periodic rate equal to a year's worth - multiplying it by the number of periods in just one year. This means that i has been calculated as a periodic rate, and not an annualized rate. N in your calculator would be 3 (years).Īlthough APR seems simpler on paper when you use the calculator inputs to figure i you use the total amount of compounding periods. Since the EAR equation looks at the whole investment horizon, and interpolates an annualized return for that whole time frame, when using the calculator, you don't need to account for however many compounding periods there are, just the length of the investment horizon in years. The calculator doesn't care or keep track of whether you are actually inputting n or m, it's up to you to figure out your time period, but remembering this can actually save you a little time and frustration while using the calculator. What you should also keep in mind is that the TMV programs in the calculators use an input called N. So if you invest money for 3 years compounding quarterly, m=4 n=12 There is also another time period called n the difference being that m is the number of periods/year, and n is the total number of periods for the investment. In the paper formulas you'll see that each equation uses m to denote the period. It is also used to compare investments with different time horizons like for example 3 years 7% compared to 5 4%. It takes the apples and oranges of periodic monthly, quarterly, semiannually compounding rates and transforms them into apples and apples on a yearly basis. Since EAR does account for compounding periods, it is used when comparing investments that have different compounding periods.
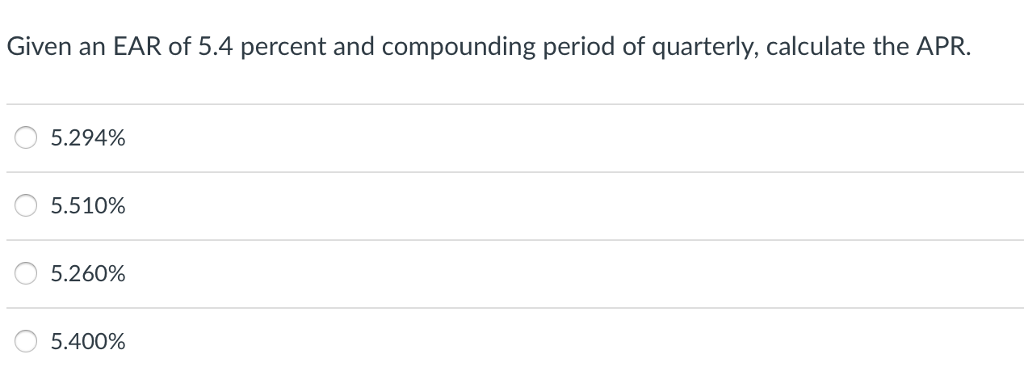
0 kommentar(er)
